【千葉県数学】関数トレンド対策 Vol.1「平行四辺形の構築」（石川県2025参考・オリジナル問題）

千葉県公立入試の数学における最新トレンドは、「パターンB（座標を文字で置き、図形を構築する）」であることは前回の記事で解説した通りだ。

「千葉県の過去問はもう解いてしまった」 「もっとこのパターンの初見問題を練習したい」

そんな意欲ある受験生のために、習志野受験研究所では、全国の入試問題を分析し、千葉県型に再構成した「完全オリジナル問題」を作成した。

第1回は、2025年（令和7年度）石川県の問題をベースに、千葉県で頻出の誘導形式にアレンジしたものだ。 この問題を解いて、「座標で図形を作る感覚」を養ってほしい。

---

▼実戦トレーニング Vol.1

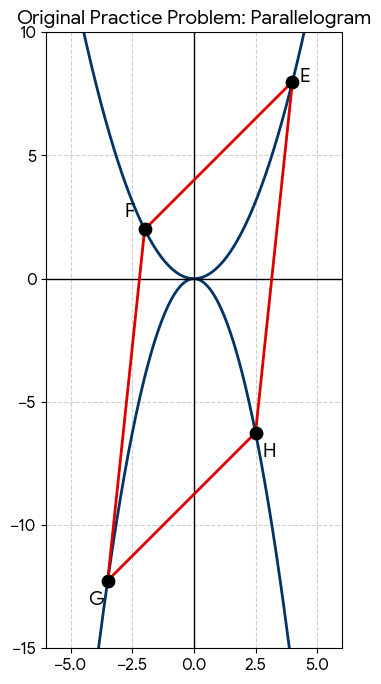
関数 $y=\frac{1}{2}x^2$ のグラフ上に点E, Fがあり、関数 $y=-x^2$ のグラフ上に点G, Hがある。

点E, Fの $x$ 座標はそれぞれ $4, -2$ であり、四角形EFGHは平行四辺形である。

このとき、次の(1), (2)の問いに答えなさい。

(1) 点E, Fの座標をそれぞれ求めなさい。

(2) 点Gの座標を求めなさい。

---

▼研究所からのヒント

いきなり答えを見る前に、まずは方針を立てよう。

1. 座標を確定させる（誘導に乗る）(1)はサービス問題だ。まずは点Eと点Fの座標を数字で出してしまおう。
2. 「平行移動」で考える平行四辺形ということは、向かい合う辺は平行で、長さも等しい。つまり、「点Fから点Eへの移動（右にいくつ、上にいくつ？）」と同じ動きを、「点Gから点Hへ」もしているはずだ。
3. 文字で置く点Gの $x$ 座標を $t$ （または $g$）と置いてみよう。ヒント2を使えば、点Hの座標も $t$ で表せるはずだ。
   
   

---

本番への教訓

千葉県入試でも、「平行四辺形」や「ひし形」を作る問題は頻出だ。 その際、直線の式を出して交点を計算する…といった遠回りは命取りになる。

今回のように「座標の移動（右にいくつ、上にいくつ）」に着目し、文字を使って方程式を立てる解法（パターンB）をマスターしておこう。 これが時短と正確性を両立する、上位校合格者の解き方だ。

※本問は、石川県2025年度入試問題を参考に、習志野受験研究所で数値を変更・再構成したオリジナル問題である。

---

運営者より：実戦演習のススメ

この問題の元となった実際の入試問題（石川県）や、さらに多くの類題演習を行いたい場合は、当塾の授業にて配布している。 「解き方」を知るだけでなく、「自分の手で解ける」ようになるまで徹底的にトレーニングしよう。

関連記事：【千葉県数学】関数トレンド対策 Vol.2「長方形の構築」（岩手県2025参考・オリジナル問題）