【千葉県公立入試】数学大問2（関数）は「計算」ではない。「パターン認識」で瞬殺せよ。

千葉県公立入試の数学において、受験生の明暗を分ける「魔の時間帯」がある。
それが、大問2の「関数」だ。

(1)の基礎問題は、ほとんどの受験生が解ける。
しかし、続く (2) で手が止まり、ここで5分、10分と時間を溶かしてしまう受験生が後を絶たない。

結果として、後半の図形や規則性に回す時間がなくなり、平均点前後に沈んでしまう。

しかし、断言する。
千葉県の関数問題は、「その場で一から考える」問題ではない。
もちろん、パターンを身につけるまでには練習が必要だが…「知っているパターンに当てはめる」だけの作業である。

習志野受験研究所では、過去14年分の過去問から、出題される「3つの黄金パターン」を整理した。

---

パターンA：等積変形（面積を移動させる）

「△OAB と △PAB の面積が等しくなるような点Pを求めよ」
といったタイプの問題である。

千葉県入試において「面積が等しい」というワードが出たら、まずは「平行線（等積変形）」を疑うのが鉄則だ。
「傾きが同じ直線」を引くだけで、ゴリゴリ計算しなくても答えの座標が見えてくる。

---

パターンB：座標を t と置く（図形構築）

「グラフ上に正方形や長方形を作る」問題がこれにあたる。
このとき、「座標がわからないから解けない」と嘆くのはナンセンスである。

わからないものは文字で置けばいい。
点Aのx座標を t と置き、すべての座標を t で表す。
あとは「辺の長さが等しい（正方形）」などの条件から方程式を立てるだけだ。

この「とりあえず t と置く勇気」が、上位校合格へのパスポートとなる。

---

パターンC：面積比と座標の関係

「面積が2倍になるときの座標を求めよ」
といったパターンである。

これは、まともに面積を計算しまくるのではなく、
「底辺の比＝面積の比」を利用するケースが圧倒的に多い。
y軸やx軸を「底辺」と見なし、その長さ（または比）から座標を逆算する。

---

▼【研究所独占分析】千葉県入試、関数の「歴史」が変わった

過去14年間の出題データを分析すると、千葉県の関数問題には、はっきりとした「流行の移り変わり」が見えてくる。

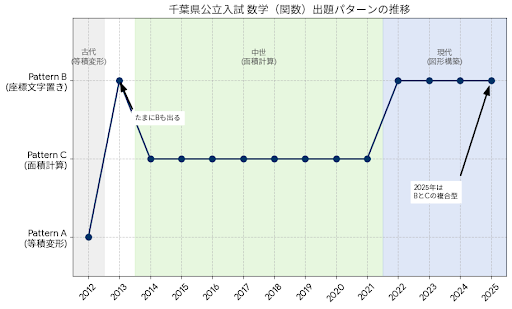
古代（2012年頃）：等積変形を正面から問う時代
2012年前後には、「平行線を引いて面積を移動させる（パターンA）」こと自体をテーマにした問題が出題されていた。
ただし、このタイプが主役だったのはごく短い期間で、その後は単体での出題はほとんど見られない。

中世（2014年〜2021年）：面積計算・面積比の時代
この期間の中心は、「面積を計算させる（パターンC）」タイプだ。
「面積比が〇：〇になる座標を求めよ」「面積が○倍になる点を求めよ」といった問題が多く、面積を式にして整理する力が問われていた。
（一部の年度では、座標を文字で置くパターンBも顔を出している。）

現代（2022年〜現在）：座標文字置き（構築）の時代
2022年以降はトレンドがはっきり変わった。
「正方形を作れ」「平行四辺形を作れ」といった、図形の性質を利用して座標を文字で置く（パターンB）問題が続いている。
2025年度は、Bに加えて面積条件（C）も組み合わせた“複合型”になっており、B・C両方の力が求められている。

---

【結論】今の受験生がやるべきこと

過去問を解くとき、2014〜2021年あたりの問題だけを見て
「面積計算ばっかりだな」と安心しないこと。

最新の傾向では、
「座標を t と置き、正方形・平行四辺形などの図形をグラフ上に構築する力」
が鍵になっている。

ここを重点的に鍛えることが、令和8年度入試を突破するための現実的な対策になる。

---

▼千葉県公立入試「関数」完全攻略ロードマップ

「結局、どの年度の過去問をやればいいの？」
そう迷う受験生のために、研究所が推奨する「最短ルートで力をつける学習順」を公開する。

手当たり次第に解くのではなく、この順番で「脳の回路」を作っていってほしい。

---

【Step 1】まずはここから！「座標を文字で置く」入門編

いきなり難しい図形に行くと挫折するので、まずは
「座標を t（や p）と置いて、長さを表して方程式を作る」感覚に慣れよう。

• 推薦問題：2015年（前期）
  線分QRの長さが3cmになる座標を求める問題。
  シンプルで、「座標文字置き」の練習に最適。
• 推薦問題：2021年
  平行四辺形の面積が指定された値になるように座標を求める問題。
  等積変形の考え方も絡むが、基本は「座標を使って底辺と高さを表す」こと。Step 2への架け橋になる良問だ。

---

【Step 2】絶対に落とせない！「トレンド（パターン B）」完答セット

ここが最重要だ。直近3年分の過去問は、暗記するくらい解き直し、
「正方形・長方形・平行四辺形」を作る手順を身体に染み込ませること。

• 必須：2022年（長方形）
  合同な長方形を作る。座標の対称性を利用する。
• 必須：2023年（正方形）
  正方形ABCDを作る。一番オーソドックスな「ザ・千葉県」問題。
• 必須：2024年（平行四辺形）
  線分の長さの関係式から座標を逆算する。

指導のポイント：
解けたかどうかではなく、「初手で点Aの座標を (t, at²) と置けたか？」をチェックしよう。
手が止まっていたら、そこを徹底的に矯正する必要がある。

---

【Step 3】上位校（偏差値60以上）狙い！「複合型」への挑戦

Step 2まで完璧なら、偏差値55前後の高校は合格点だ。
船橋・東葛・千葉東・薬園台・佐倉などを狙う生徒は、さらに「面積計算（パターン C）」の処理能力を足そう。

• 挑戦：2025年（最新）
  パターン B（文字置き）とパターン C（面積方程式）の融合。
  これが解ければ免許皆伝だ。
• 練習：2018年
  台形と平行四辺形の面積比。計算が少し重いが、これをやり切る計算力が「最後の粘り」を生む。

---

さいごに：過去問演習で「道具」を手に入れよう

ただ漫然と過去問を解くのではなく、
「今のトレンド」を意識して解くことで、学習効率は何倍にもなる。

「過去問を年度別にバラすのが大変」
「自分の解き方が合っているか不安」

という生徒のために、当塾（Assist習志野校）では、この「黄金パターン別・過去問特訓セット」を製本して塾生に配布している。

最短ルートで関数を極めたい君は、ぜひ教室の扉を叩いてほしい。
我々は「解き方」だけでなく、「合格への近道」を用意して待っている。

---

※（注意）🚫 優先度を下げてよいリスト

以下の問題は今のトレンドと少しズレるため、時間に余裕がない場合は後回しでも構わない。

• 2012年（前期）
  純粋な等積変形。今はここまで単純なのは出ない。
• 2016年以前の「面積比」特化問題
  難易度が高い割に、最近の出題傾向（図形構築）とは少し離れているため。
  
  時間と心に余裕が出てきたら、仕上げとして挑戦してみよう。

【NEW】2025.11.21 追記 この記事で解説した「パターンB」を実際に練習できる、オリジナル演習問題（Vol.1）を公開した！ 偏差値60以上を狙う君は、今すぐ解いてみよう。

▶【千葉県数学】関数トレンド対策 Vol.1「平行四辺形の構築」はこちら

【NEW】2025.11.24 追記 さらに続けて「パターンB」を実際に練習できる、オリジナル演習問題（Vol.2）も公開した！ 「自分の手で解ける」ようになるまで徹底的にトレーニングしよう。

▶【千葉県数学】関数トレンド対策 Vol.2「長方形の構築」（岩手県2025参考・オリジナル問題）