※本記事は、客観的分析のため『だ・である調』で統一しています。
【千葉大数学2025 詳細分析】難問より「完答力」。学部ごとの「捨ててはいけない一問」を徹底解剖
2025年度千葉大学(前期)の数学は、全体として「難問奇問は少ないが、高い計算精度と記述力が求められるセット」であった。
一見すると解きやすそうな問題が並ぶが、最後まで正解に到達するには相当な計算力と持久力が必要になる構成である。
本稿では、まず複雑な学部ごとの出題区分を整理し、そのうえで「どの問題を落とせないか」という観点から合否を分けた要因と次年度への指針をまとめる。
1.全体概況:2024年度との比較
難易度は、おおむね昨年並み〜やや易化。ただし計算量と記述量はむしろ増加傾向にある。
標準的な分野を幅広くカバーする構成は例年通りであり、
数I・II・A・B・C(ベクトル)+数IIIからバランスよく出題されている。
これまでの「思考力重視」に加えて、
- 数IIIの重厚な計算(第6・7問)
- 場合の数の丁寧な数え上げ(第5問)
といった処理能力を問う問題が合否を分けたセットといえる。
2.【前提】受験区分別・解答指定と試験時間
千葉大数学の最大の特徴は、学部・学科によって
- 解答すべき大問
- 試験時間
が大きく異なる点にある。分析を読む前に、自分の志望区分がどこに属するかを確認しておきたい。
受験区分別 早見表(概要)
| 区分 | 主な学部・学科 | 試験時間 | 解答大問 | 特徴 |
|---|---|---|---|---|
| 文系・教育(非数学) | 文、法政経、国際教養、教育(小・英など)、園芸(食料)など | 80分 | [1]〜[3] | 数I・II・A・B・C(ベクトル)中心の基礎〜標準セット。全問完答を狙える難易度。 |
| 理工・薬・園芸・理(非数学) | 工、薬、園芸(緑地など)、理(物理・化学など)、情報データサイエンス など | 120分 | [4]〜[8] | 数IIIを含む標準的な理系セット。問題冊子に載っている[1]〜[3]は解答不要。 |
| 医学部医学科 | 医 | 120分 | [5]〜[9] | 易しめの導入問題がなく、いきなり確率・数IIIから始まる最難関セット。 |
| 理学部(数学・情報数理) | 理(数学・情報数理) | 180分 | [4]〜[9] | 理工系セット+難問[9]までを解き切る「最多演習セット」。体力勝負。 |
| 教育(数学科) | 教育(数学) | 150分 | [3]〜[8] | 文系用[3]と理系用[4]〜[8]が混在する変則セット。 |
冊子を開いたときに「どこから始めるか」を間違えると、その時点で時間配分が崩れる。
特に理工系は [1]〜[3]に一切触れない というルールを、事前に身体にしみ込ませておきたい。
3.学部別・合否を分ける「勝負問」
3-1.文系・教育系(問題 [1]〜[3])
構成:
[1] 常用対数/[2] 3次方程式+確率/[3] ベクトル
勝負の分かれ目:2完+α の確保
第1問・第2問は教科書章末レベルの基礎問題であり、ここでの失点はそのまま合否に直結する。
文系セットで最も差がついたのは第3問(ベクトル)である。
正三角形と内接円をベクトルで扱う設定の中で、誘導に乗りながら計算を最後まで合わせ切れたかどうかが合格の鍵になった。
3-2.理工・薬・園芸・一般理系(問題 [4]〜[8])
構成:
[4] 数列/[5] 確率/[6] 微積(数III)/[7] 関数(数III)/[8] 複素数平面
勝負の分かれ目:第6問・第7問の完遂力
第4問(数列)と第5問(確率)は、理系受験生なら完答しておきたい標準レベル。
この2問で取りこぼしが多いと、合格は厳しくなる。
合否を分けたのは第6問(対数と面積)と第7問(関数のグラフ描画)である。
特に第7問は計算量が多く、ここを120分の試験時間内で処理しきれたかどうかが、数学得意層とそうでない層を分けた。
3-3.医学部医学科(問題 [5]〜[9])
構成:
[5] 確率/[6] 微積(数III)/[7] 関数(数III)/[8] 複素数平面/[9] 積分不等式
勝負の分かれ目:ミスの許されない高得点勝負
[5] からすでに本番レベルであり、[5]〜[7]については完答が前提となる。
そのうえで、
- 第8問(複素数平面の幾何的考察)を手早くまとめられたか
- 最難関の第9問(不等式証明)で (1)〜(2) の部分点をどこまで積み上げられたか
がボーダー付近の合否を分けたと考えられる。
4.大問別 詳細分析と計算の勘所
4-A.文系・共通範囲:第1問〜第3問
第1問(桁数・最高位)
$12^{77}$の桁数と最高位を求める問題。
$\log_{10}2, \log_{10}3$ の近似値を用いて評価するだけでよく、教科書レベルの基本動作が身についていれば完答できる。
第3問(ベクトル)
正三角形の内接円上の点 $P$ に対し、内積 $\vec{PD} \cdot \vec{PE}$ が一定になることを示す問題。
重心(原点)を始点とするベクトルで整理し、
$$\vec{OA} + \vec{OB} + \vec{OC} = \vec{0}$$
という定石を自然に使えるかどうかがポイントになる。
ここが出てこないと、途中で計算が破綻しやすい。
4-B.理系標準:第4問〜第5問
第4問(数列・極限)
漸化式
$$a_{n+1} = \frac{2}{3}a_n + \frac{9}{a_n^2}$$
を題材とした不等式の証明。
(3) で現れる $a_{n}−3 $という形を作る誘導に素直に従えるかどうかが勝負であり、
難問というよりは「誘導を読み飛ばさないかどうか」を測る問題である。
この漸化式は、実は $x3=27 の解(x=3)$へ収束するニュートン法の反復を背景に持つ。
数列の計算問題でありながら、解析の一端に触れさせる良問と言える。
第5問(確率・ランダムウォーク)
サイコロの目に応じた平面上の移動を扱う問題。
- $x$ 座標:1,2 のときのみ移動
- $y$ 座標:3,4 で +1,5,6 で −1
というように、$x$ と $y$ の動きが独立していることに気づけるか、
あるいは気づけなくても、全事象を整理して数え上げきれるかがポイントになる。
数え漏らしが起きやすい構成であり、「丁寧な場合分け」と「整理力」が試される千葉大らしい一問である。
4-C.数III 計算耐久戦:第6問・第7問
第6問(対数関数・接線・面積)
円と $y=logx$ が接する条件を求め、その後に面積を計算させる問題。
パラメータ $a=\sqrt{3}$ を代入して積分まで進める必要があり、
方針自体は立てやすいものの、途中計算でミスを誘発しやすい数値設定になっている。
論理的な構成と計算精度の両方が求められた。
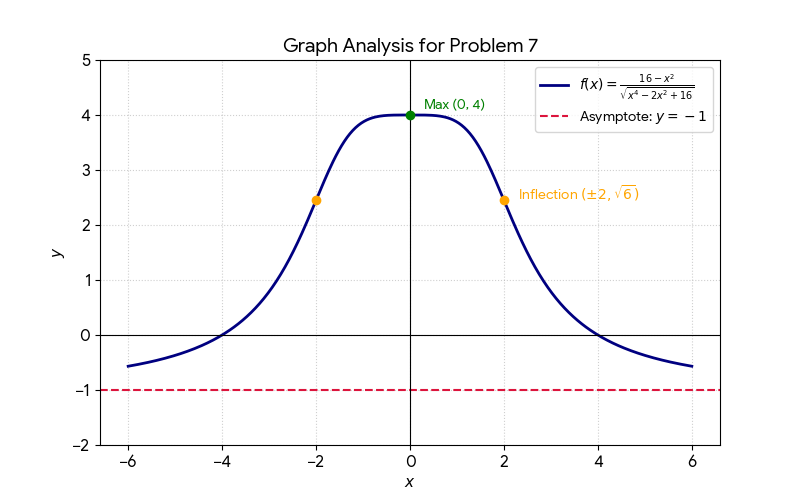
第7問(関数のグラフ・変曲点)
関数 $f(x)=\frac{16-x^{2}}{\sqrt{x^{4}-2x^{2}+16}}$
の増減・凹凸・漸近線を調べ、グラフの概形を描く問題。
一階・二階導関数の計算が重く、手計算で最後までやり切るにはかなりの体力を要する。
詳細は【付録】にまとめるが、増減表を完成させることで
- 極大値:(0,4)
- 変曲点:(±2,6)($\pm 2,\sqrt{6}$))
- 漸近線:$y=−1$
を持つベル型のグラフが導かれる。
ここまで到達できた受験生は、実戦的な数III計算力が備わっていると言ってよい。
4-D.難問枠:第8問・第9問
第8問(複素数平面)
複素数平面上で 4 点が正方形をなす条件を、複素数を用いて表現する問題。
幾何的なイメージと代数計算の両方が要求され、得意不得意の差が直に表れる。
第9問(積分・不等式証明)
平均値の定理を用いて不等式を評価する、抽象度の高い問題。
設問 (4) まで完答するのは試験時間内ではかなり厳しく、
多くの受験生にとっては「(1)〜(2)で部分点を確保し、深追いしない」ことが合理的な判断になる。
今年のセットにおける「捨て問候補」は、この第9問である。
5.2026年度入試に向けた学習指針(ベースライン)
今年のセットが発信しているメッセージは明確である。
解法暗記だけでは太刀打ちできないが、突飛なひらめきも要求されない。
必要なのは、標準的な問題を最後まで解き切るための、正確でタフな運用能力である。
その観点から、学習の軸を三つに整理しておく。
5-1.「最後まで解き切る」訓練
第6問・第7問のように、式が複雑になっても途中で筆を止めず、
増減表や面積計算を最後まで書き切る計算持久力を鍛える必要がある。
過去問演習では、答えが出る直前で解説に頼るのではなく、
多少時間がかかっても「自分の手で完答する」経験を積んでおきたい。
5-2.過去問演習での「捨て問・取り問」の選別
特に医学部・理学部数学科以外の受験生は、第9問のような難問に時間を使いすぎない訓練が不可欠である。
- 自分の得点源となるレベルの問題を見極める
- それ以外の問題には、最初から「(1)だけ」「誘導の途中まで」といった目標を設定する
といった時間戦略を、実際の過去問の中で試しておきたい。
5-3.論証力の強化
「示せ」「証明せよ」という形式の問題が多いため、
独りよがりな式変形ではなく、採点者に論理の流れが伝わる記述が必要になる。
- 何を示したいのかを最初に一文で書く
- 式変形の根拠(単調性、大小関係など)を簡潔に添える
といった基本を、学校の定期テストや模試の復習段階から意識しておきたい。
6.【実戦】「今年はこう動くべきだった」立ち回りシミュレーション
ここからは、実際の試験本番でどう動くべきだったかを、モデルケースで簡単にシミュレーションしておく。
6-1.医学部志望モデルケース(120分・問題[5]〜[9])
パターンA:合格圏に乗る理想的な立ち回り
- [5] 確率:完答(〇)
- [6] 微積:完答(〇)
- [7] 関数:途中まで(極大値・変曲点まで)解いて部分点(△)
- [8] 複素数平面:主要な設問まで完答(△〜〇)
- [9] 不等式: (1)(2) のみ解いて部分点確保(△)
時間配分イメージ
- [5]+[6] で 60〜70分
- [7] で 25〜30分
- [8] で 15〜20分
- [9] で 10分前後((1)(2)を取り切って撤退)
→ [5]〜[8] の得点率が高ければ、[9] 完答がなくても十分に合格圏に乗る。
パターンB:危険な立ち回り
- [5]・[6] で計算ミスが出て取りこぼす
- [7] を「どうしても完答したい」と粘りすぎて 40〜50分投入
- その結果、[8] の着手が遅れ、[9] までたどり着かない
問題点
- 「得点効率のよい標準問題」よりも、「時間単価の高い難問」に時間を割きすぎている。
- 特に第8問は設問構成がコンパクトで、短時間でもきちんと点数になるため、ここを落とすとダメージが大きい。
来年度に向けては、「第7問をどこまでやったら一度区切るか」「第8問に最低何分は残すか」といった “撤退ライン” を事前に決めておくこと が重要になる。
7.第7問タイプに備える「教材ゾーン」の目安
第7問のような「数III・グラフ総合問題」に対応するには、次の三段階を意識しておきたい。
- 基礎:教科書例題〜標準問題集の微分・グラフ範囲
- 一次・二次関数、指数・対数関数、三角関数の増減・極値・凹凸を、自力でグラフに起こせるレベル。
- 応用:入試標準レベルの「グラフ総合」問題
- 無理関数や分数関数を含む問題で、
- 偶奇性の判定
- 漸近線の計算
- 変曲点・極値の整理
までを一問の中で処理する練習を積む。
- 無理関数や分数関数を含む問題で、
- 仕上げ:実際の国公立・難関私大の過去問
- 千葉大本番と同じく、「グラフの概形を描け」と要求される問題で、
増減表→概形スケッチ までを時間を測って解く。
- 千葉大本番と同じく、「グラフの概形を描け」と要求される問題で、
具体的な教材名は塾で相談して決めればよいが、
目安としては「共通テスト標準〜国公立二次標準レベル」の問題集の
- 数III・微分法の応用
- グラフ総合(極限・微分・積分が混ざる章)
あたりをきちんとやり切れていれば、第7問タイプへの土台は十分と考えてよい。
8.理系/医・数情向け「1年計画」の骨組み
最後に、理工系・医学部・理学部(数学・情報数理)を志望する受験生向けに、
千葉大数学を見据えた ざっくり1年ロードマップ を置いておく。
春(〜5月):数IIIの基礎固め
- 学校の進度を先取りしつつ、
- 微分法:基本公式/接線・極値まで
- 積分法:計算の基本パターン
を教科書レベルで固める。
- この段階では、まだ千葉大過去問には触れなくてよい。
「公式を見ないで使える」状態を目標にする。
夏(6〜8月):千葉大レベルの典型演習
- 数I・II・A・B の典型問題+数IIIの応用問題を並行して演習する。
- 目標は、
- 第4問レベルの数列/不等式
- 第5問レベルの確率
- 第6・7問の簡略版(計算量を少し抑えた総合問題)
を、解説を見れば理解できるレベル に持っていくこと。
秋(9〜11月):過去問+時間配分訓練
- 千葉大数学の過去問に本格的に取り組む。
- 最初は「時間無制限」で丁寧に完答まで追い、
次第に 本番と同じ時間制限(80・120・150・180分) を意識して演習する。 - この時期に、前述の
- 「どの大問を必答にするか」
- 「どこで撤退するか」
といった自分なりのルールを固めておく。
冬(12〜入試直前):弱点補強+シミュレーション
- 過去問演習で見えてきた
- 単元ごとの抜け(例:数列の評価・ベクトルの内積計算など)
- 時間配分の癖
を、ピンポイントに補強する。
- 週に1回程度は、本番と同じ条件で “模擬千葉大数学” を実施し、
得点だけでなく「立ち回り」を振り返る。
【付録】第7問のグラフ形状解析
第7問の関数 $f(x)=\frac{16-x^{2}}{\sqrt{x^{4}-2x^{2}+16}}$
について、計算を進めることで、グラフは次のような特徴を持つことが分かる。
これらをすべて押さえた受験生が、完答レベルに到達したとみなせる。
1.対称性
関数式には $x^2, x^4$ の項しか含まれないため、$f(x)$ は偶関数となる。
したがって、グラフは $y$ 軸対称になり、解析は $x≥0$の範囲に絞ってよい。
2.極限と漸近線
$x \to \infty$ のとき、分子・分母を $x^2$ で割って極限をとると
$$\lim_{x \to \infty} f(x) = -1$$
となる。
よって、グラフの両端は直線 $y = -1$ に近づき、この直線が水平漸近線になる。
3. 増減・変曲点と概形
一階・二階導関数を用いて増減表を作成すると、次の性質が得られる。
- 極大値:点 $(0, 4)$ で最大値をとる。
- 変曲点: $x = \pm 2$ で $y = \sqrt{6}$ となる 2 点が変曲点になる。
これらを踏まえると、グラフの概形は次のようにまとめられる。
- $y = -1$ 付近から立ち上がり、$(0, 4)$ をピークとする
- 変曲点 $(\pm 2, \sqrt{6})$ を通過しながら緩やかに下降する
- 再び $y = -1$ に近づいていく「ベル型(釣鐘型)」の曲線になる
下図のような形を自力で描き切れたかどうかが、第7問完答の分かれ目になったと考えられる。
▼具体的な対策(ロードマップ)はこちら
過去問を見て絶望した君へ。高1・高2から始める「千葉大数学」攻略ロードマップ 〜「才能」はいらない。「計算の体力」をつけろ〜






コメント