【千葉県数学】関数トレンド対策 Vol.2「長方形の構築」（岩手県2025参考・オリジナル問題）

好評の「千葉県型・数学厳選トレーニング」、第2弾を公開する。
前回は「平行四辺形」だったが、今回は「長方形（正方形）」を作るパターンだ。

千葉県入試では、2022年に「長方形」、2023年に「正方形」を作る問題が連続して出題されている。
図形の名前が変わっても、やるべきことは「座標を文字で置く（パターンB）」一択だ。

今回の問題は、2025年（令和7年度）岩手県の問題をベースに、千葉県で頻出の「周の長さ」を条件にした形式にアレンジした。

▼実戦トレーニング Vol.2

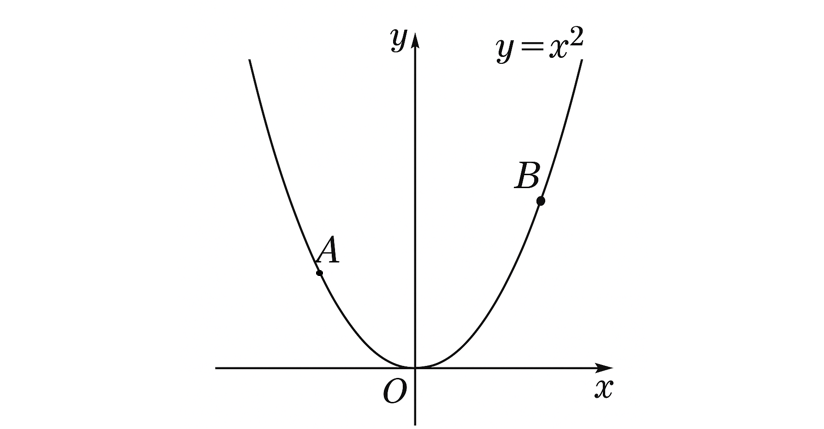
関数 $y=x^2$ のグラフ上に点 A, B がある。
点 A の $x$ 座標は $-2$ であり、点 B の $x$ 座標は正である。
線分 AB を対角線とし、各辺が $x$ 軸、$y$ 軸に平行な長方形を作るとき、次の問いに答えなさい。

(1) 点 A の座標を求めなさい。
(2) この長方形の周の長さが 20 になるとき、点 B の座標を求めなさい。

▼研究所からのヒント

• 点Aを確定させる
  まずは点 A の座標を数字で出してしまおう。これがスタートラインだ。
• 点Bを文字で置く
  点 B は $y=x^2$ 上にある。「$x$ 座標を $t$」と置けば、$y$ 座標は $t^2$ で表せるはずだ。
• 「縦」と「横」の長さを $t$ で表す
  長方形の周の長さは「(縦＋横) × 2」 で求められる。
  横の長さ ＝ B の $x$ 座標 − A の $x$ 座標
  縦の長さ ＝ B の $y$ 座標 − A の $y$ 座標
  これを使って方程式を立てよう。

本番への教訓

「周の長さ」や「面積」といった条件が与えられたら、まずは座標を $t$ で置き、長さを $t$ の式で表すこと。この手順さえ守れば、どんな図形が来ても怖くない。

今回の問題は、計算結果がたまたま「正方形（縦と横が同じ）」になったが、入試では「正方形になるときの座標を求めよ」と最初から指定されることも多い。その場合は
「縦の長さ ＝ 横の長さ」
という方程式を立てればよい。

※本問は、岩手県2025年度入試問題を参考に、習志野受験研究所で数値を変更・再構成したオリジナル問題である。

---

運営者より：実戦演習のススメ

「解き方」を知るだけでなく、「自分の手で解ける」ようになるまで徹底的にトレーニングしよう。
当塾では、こうした「千葉県特有のトレンド」に合わせた類題演習を数多く用意している。